Assessment of beet quality from fixed sucrose/nonsucrose ratios (rendement factors) of molasses.

M. Burba and H. Harling, Zuckerindustrie (2003), pp. 233-242, 508-513, 745-750 (German).

On page 511 of this article the authors write that my (former) group does not adhere to the "principles of the rendement method". I want to explain why I personally disagree. Sorry for that, but a contrary point of view should be possible in a scientific discussion:

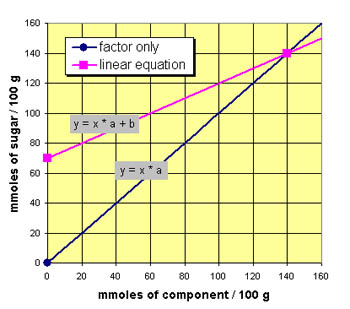The application of a factor (rendement factor, ratio) is a special form of linear equation y = x * a, which passes the point of origin. But the zero/zero-condition is not fulfilled with nonsugar components, such as alkalis, nitrogen or ash. If the zero/zero-condition is not true, the constant is different from zero and the slope of the "factor-equation" is too steep. Blomberg, Swietlicka and Tjebbes (CITS 1983) examined "additional moles of sucrose" versus "additional moles of sodium" and they found a slope considerably lower than 1.

Rendement factors for nonsugar components cannot be used as a slope of a linear equation with a constant of zero. Only the total nonsugar can be used this way, because in a pure sucrose solution (nonsugar = zero) no sugar is kept in solution:
false:	no alkalis = no molasses sugar
false:	no nitrogen = no molasses sugar
false:	no alkalies and no nitrogen = no molasses sugar
true:	no nonsugar = no molasses sugar
Beet quality formulas are often a matter of policy with a lot of prestige instead of pure science. Beside prestige, old formulas with good effect on beet quality improvement are used, independent of their wrong scientific background. But wrong preconditions of beet quality formulas should not influence sugar technology science and lead to the wrong calculation of losses and payback of investment in the future. The authors give a new precondition for molasses in their equations (1) (2) (3) and they stress the validity of both, the Dedek-factor and the Anderlik-factor. The following identical formulas are shown in the paper (m=mass,  w'=moles per mass,  S=sucrose,  Me=molasses): mS,Me = 0,342 * w'(K+Na),Me   and   mS,Me = 0,342 * w'N,Me The authors adopt these two "factor-equations" and add them up as follows: 2 * mS,Me  =  0,342 * w'(K+Na),Me   +   0,342 * w'N,Me They don't realize that with these 3 equations they state even for non exhausted molasses:   w'(K+Na),Me  =  w'N,Me     or verbally:   the moles of alkalis in any molasses correspond to the moles of harmful nitrogen. The question arises why the authors use both alkalis and nitrogen although alkalis are equal to nitrogen, according to them. If a = b, it is simpler to use  a  or  b  instead of  ½ a  +  ½ b. Normally scientists try to shorten mathematical equations, which is the contrary of complicating matters. The precondition of the authors with addition of two bisected rendements seems to be wrong, but uncertainties of beet quality calculations lead to a result similar to that of other authors. I think the first equation of the summary of the paper requires a constant, which would represent "carbohydrates minus sucrose" and belongs neither to salts nor to nitrogen compounds, although this remainder (dextran, gums, laevan, raffinose, galactinol, kestoses etc.) might have a low melassigenic effect. I doubt that sucrose can be fully separated by crystallisation from these carbohydrates and there should be at least a small average constant, otherwise the slopes for alkalies and N will again become too steep.

Relationship (?) between alkalis and sucrose  (values calculated from table 3 of the paper) The "regression scientists" mostly get different results along the distance between "low value beet" and "high value beet", and if not they cannot draw conclusions from "their c l o u d". The "factor scientists"  a) should not suppose a zero/zero-condition, if this is obviously wrong and   b) work with "low value composition" and "high value composition", otherwise they cannot conclude very much from "their average composition".

2003-11-29      G. Pollach