 On page 699, third chapter "Calculation of the quantity of molasses sugar", some disadvantages of regression analyses of other authors, including our group, are mentioned.
As a consequence of this, a model partly based on Dedek's alkali factor was preferred, but with a wrong quotation of Dedek's paper. This error could be copied further and should be clarified. Dedek claimed a ratio of 1 mol of sucrose in exhausted molasses per 1 mol of alkalis in exhausted molasses - and not a ratio of 1 mol sucrose in exhausted molasses (on beet) per 1 mol of alkalis in beet. Due to the degree of alkali extraction, 1 mmol of alkalis will retain about 0.85 mmoles of sucrose in molasses (on beet). This error of quotation may have been stimulated by an earlier paper of Wieninger and Kubadinow with erroneous examples.
On page 699, third chapter "Calculation of the quantity of molasses sugar", some disadvantages of regression analyses of other authors, including our group, are mentioned.
As a consequence of this, a model partly based on Dedek's alkali factor was preferred, but with a wrong quotation of Dedek's paper. This error could be copied further and should be clarified. Dedek claimed a ratio of 1 mol of sucrose in exhausted molasses per 1 mol of alkalis in exhausted molasses - and not a ratio of 1 mol sucrose in exhausted molasses (on beet) per 1 mol of alkalis in beet. Due to the degree of alkali extraction, 1 mmol of alkalis will retain about 0.85 mmoles of sucrose in molasses (on beet). This error of quotation may have been stimulated by an earlier paper of Wieninger and Kubadinow with erroneous examples.
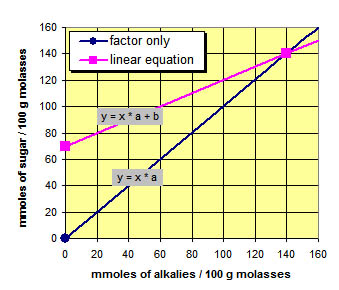 But there is a further error in all concepts which are at least partly based on the Dedek-factor:
The application of a factor (ratio) is a special form of linear equation y = x * a,
which passes the point of origin. But this is a wrong assumption. Due to the increasing viscosity, sucrose cannot be totally exhausted from impure syrups, not even after the total removal of alkalis. The residual sucrose (which cannot be determined under practical conditions) represents the constant of a linear equation with realistic slope. Blomberg, Swietlicka and Tjebbes (CITS 1983, p. 483) examined "additional moles of sucrose" versus "additional moles of sodium" in sugar syrups and they found a slope considerably lower than 1. This is relevant for the calculation of f in chapter 3.1 too. But there is a further error in all concepts which are at least partly based on the Dedek-factor:
The application of a factor (ratio) is a special form of linear equation y = x * a,
which passes the point of origin. But this is a wrong assumption. Due to the increasing viscosity, sucrose cannot be totally exhausted from impure syrups, not even after the total removal of alkalis. The residual sucrose (which cannot be determined under practical conditions) represents the constant of a linear equation with realistic slope. Blomberg, Swietlicka and Tjebbes (CITS 1983, p. 483) examined "additional moles of sucrose" versus "additional moles of sodium" in sugar syrups and they found a slope considerably lower than 1. This is relevant for the calculation of f in chapter 3.1 too.
The final equations of the paper were included in an updated table of molasses sugar coefficients from different authors on this web-site. The αN factor of the author is zero if K+Na-αN >= 35 mmol/kg beet. In case of the alternative calculation (< 35) it is a little lower than most of the other factors, established via multiple regression. This could be explained by some parallel increase of αN and betain. The effect of the latter one is detected via thick juice purity determination in the regression approach and any parallelism will cause an increase of the αN-factor. The good agreement of factors derived from multiple regression with factors derived from theoretical considerations shows that alkalis and αN seem to be rather independent.
|
|
2005-04-16 G. Pollach
|


 On page 699, third chapter "Calculation of the quantity of molasses sugar", some disadvantages of regression analyses of other authors, including our group, are mentioned.
As a consequence of this, a model partly based on Dedek's alkali factor was preferred, but with a wrong quotation of Dedek's paper. This error could be copied further and should be clarified. Dedek claimed a ratio of 1 mol of sucrose in exhausted molasses per 1 mol of alkalis in exhausted molasses - and not a ratio of 1 mol sucrose in exhausted molasses (on beet) per 1 mol of alkalis in beet. Due to the degree of alkali extraction, 1 mmol of alkalis will retain about 0.85 mmoles of sucrose in molasses (on beet). This error of quotation may have been stimulated by an earlier paper of Wieninger and Kubadinow with erroneous examples.
On page 699, third chapter "Calculation of the quantity of molasses sugar", some disadvantages of regression analyses of other authors, including our group, are mentioned.
As a consequence of this, a model partly based on Dedek's alkali factor was preferred, but with a wrong quotation of Dedek's paper. This error could be copied further and should be clarified. Dedek claimed a ratio of 1 mol of sucrose in exhausted molasses per 1 mol of alkalis in exhausted molasses - and not a ratio of 1 mol sucrose in exhausted molasses (on beet) per 1 mol of alkalis in beet. Due to the degree of alkali extraction, 1 mmol of alkalis will retain about 0.85 mmoles of sucrose in molasses (on beet). This error of quotation may have been stimulated by an earlier paper of Wieninger and Kubadinow with erroneous examples.  But there is a further error in all concepts which are at least partly based on the Dedek-factor:
The application of a factor (ratio) is a special form of linear equation y = x * a,
which passes the point of origin. But this is a wrong assumption. Due to the increasing viscosity, sucrose cannot be totally exhausted from impure syrups, not even after the total removal of alkalis. The residual sucrose (which cannot be determined under practical conditions) represents the constant of a linear equation with realistic slope. Blomberg, Swietlicka and Tjebbes (CITS 1983, p. 483) examined "additional moles of sucrose" versus "additional moles of sodium" in sugar syrups and they found a slope considerably lower than 1. This is relevant for the calculation of f in chapter 3.1 too.
But there is a further error in all concepts which are at least partly based on the Dedek-factor:
The application of a factor (ratio) is a special form of linear equation y = x * a,
which passes the point of origin. But this is a wrong assumption. Due to the increasing viscosity, sucrose cannot be totally exhausted from impure syrups, not even after the total removal of alkalis. The residual sucrose (which cannot be determined under practical conditions) represents the constant of a linear equation with realistic slope. Blomberg, Swietlicka and Tjebbes (CITS 1983, p. 483) examined "additional moles of sucrose" versus "additional moles of sodium" in sugar syrups and they found a slope considerably lower than 1. This is relevant for the calculation of f in chapter 3.1 too.
