Menu

Pollach, G.; Hein, W.; Berninger H.: Calculation of saturated molasses purities (German). Zuckerindustrie 118 (1993) pp. 785-790.    List of papers

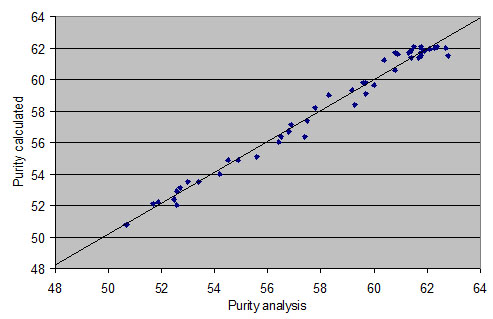
Abstract: With the aim of simplifying formulas for the calculation of saturated molasses purities, it is proposed to work on the basis of "normal temperature relationships" instead of temperature-independent "ratios of ratios". The calculation of molasses data for a given temperature then proceeds not via a single sucrose solubility number, but via pairs of solubility numbers. In that way, the familiar saturation formula can be mathematically transformed, without changing the results. If saturation equations are to take account of the nonsugar composition, in addition to temperature and the nonsugar:water ratio, it is clearer to formulate a normal temperature equation with values related to nonsugar instead of values related to water. Based on 47 analyses of "normal" and "Quentin" molasses, a multiple regression with a correlation coefficient of 0,992 was obtained. This equation, valid for 50°C, in which all values are related to nonsugar, calculates sugar per nonsugar from water and alkaline earths. An equation for the calculation of molasses purities found in the literature was transformed and compared with the results. There was good agreement in the case of normal molasses, whereas for Quentin molasses there were one-sided divergences of up to 2 purity points.

Different variants of writing the final equations A - C

S = Sugar     NS = Nonsugar     W = Water     AE = Alkaline Earths (Ca+Mg)

DM = Dry Matter     qX/Y = mass ratio     q = qS/DM = purity    w = mass fraction

w' = Molar concentration

A)

S/NS (50°C) = f1 x W/NS + f2 x AE/NS + Const. Mass ratio S/NS in molasses, saturated at 50°C = 1.898 x Mass ratio W/NS − 0.179 x ½ mmol AE per g of NS + 0.745 qS/NS,sat,50 = 1.898 x qW/NS − 0.179 x w'AE/w NS + 0.745 Example (60°C trial) 0.986 = 1.898 x 0.326 − 0.179 x 2.113 + 0.745

B)

S/NS (t°C) = S/NS (50°C) x (146.5 - 50) / (146.5 - t) Mass ratio S/NS in molasses, sat. at t°C = Mass ratio S/NS in molasses, sat. at 50°C x 96.5 / (146.5 - t) qS/NS,sat,t = qS/NS,sat,50 x 96.5 / (146.5 - t) Example (60°C trial) 1.10 (60°C) = 0.986 x 96.5 / 86.5

C)

Purity (%) = S/NS x 100 / (1 + S/NS) Mass ratio S/DM*100 in molasses, sat. at t°C = Mass ratio S/NS in molasses, sat. at t°C x 100 / (1 + Mass ratio S/NS in molasses, sat. at t°C ) qsat,t (%) = qS/NS,sat,t x 100 / (1 + qS/NS,sat,t) Example (60°C trial) 52.4 (60°C) = 1.10 x 100 / 2.10

Table 1 with three additional columns and two columns dropped

Trial no.	Code	°C	qNS/W	ysat	purity  qsat %		qS/NS,sat		qW/NS	w'AE/wNS
			analysis		analysis	calculat.	analysis	calculat.	analys.	½mmol/g
1	M01	50	2.13	1.40	62.8	61.5	1.689	1.597	0.469	0.215
2	M02	50	2.09	1.35	62.4	62.1	1.659	1.641	0.478	0.063
3	M04	50	2.08	1.33	62.3	62.0	1.650	1.633	0.481	0.140
4	M06	50	2.03	1.27	61.8	62.1	1.616	1.639	0.493	0.231
5	M07	50	2.08	1.30	61.7	61.4	1.610	1.593	0.481	0.365
6	M08	50	2.06	1.27	61.5	62.1	1.594	1.639	0.485	0.148
7	M09	50	2.08	1.29	61.4	61.4	1.593	1.590	0.481	0.382
8	M12	50	2.09	1.26	60.8	60.6	1.548	1.538	0.478	0.641
9	M13	50	2.08	1.21	60.0	59.6	1.503	1.475	0.481	1.024
10	M13	50	2.59	1.35	57.4	56.4	1.345	1.294	0.386	1.024
11	M14	50	2.05	1.22	60.4	61.2	1.528	1.579	0.488	0.516
12	M15	50	2.11	1.21	59.6	59.8	1.477	1.488	0.474	0.873
13	M16	50	2.07	1.19	59.7	59.8	1.482	1.487	0.483	0.978
14	M17	50	2.10	1.19	59.3	58.4	1.458	1.405	0.476	1.358
15	M17	50	2.62	1.27	55.6	55.1	1.252	1.227	0.382	1.358
16	M21	50	2.08	1.30	61.8	62.0	1.618	1.631	0.482	0.163
17	M21	50	2.56	1.44	59.2	59.3	1.449	1.458	0.391	0.163
18	M22	50	2.10	1.30	61.4	61.8	1.593	1.618	0.476	0.169
19	M23	50	2.09	1.32	61.8	61.7	1.619	1.612	0.478	0.225
20	M24	50	2.07	1.32	62.1	61.9	1.641	1.626	0.483	0.201
21	M25	50	2.07	1.31	61.9	61.8	1.624	1.620	0.482	0.222
22	M25	50	2.57	1.48	59.7	59.1	1.482	1.444	0.389	0.222
23	M26	50	2.07	1.28	61.3	61.7	1.586	1.611	0.482	0.274
24	M27	50	2.08	1.26	60.9	61.6	1.561	1.601	0.481	0.320
25	M28	50	2.08	0.98	54.9	54.9	1.215	1.219	0.481	2.450
26	M28	50	2.61	1.04	50.7	50.8	1.027	1.033	0.383	2.450
27	M30	50	2.05	1.09	57.8	58.2	1.371	1.394	0.488	1.550
28	M30	50	2.54	1.18	54.5	54.9	1.195	1.215	0.394	1.550
29	M31	50	2.06	1.35	62.7	62.0	1.682	1.634	0.485	0.174
30	M36	50	2.07	1.30	61.8	61.5	1.615	1.600	0.484	0.357
31	M37	50	2.05	1.23	60.8	61.7	1.548	1.613	0.488	0.326
32	M37	50	2.52	1.37	58.3	59.0	1.398	1.440	0.397	0.326
33	M38	50	2.05	1.03	56.5	56.4	1.297	1.293	0.488	2.113
34	M38	50	2.62	1.10	51.9	52.2	1.079	1.090	0.381	2.113
35	M38	60	3.06	1.18	52.5	52.4	0.989	0.986	0.326	2.113
36	M39	50	2.07	1.06	56.8	56.7	1.316	1.307	0.484	1.995
37	M39	50	2.58	1.11	52.6	52.9	1.112	1.122	0.387	1.995
38	M39	60	3.22	1.20	51.7	52.1	0.961	0.976	0.310	1.995
39	M40	50	2.09	1.05	56.4	56.0	1.294	1.272	0.479	2.133
40	M40	50	2.58	1.11	52.5	52.4	1.106	1.100	0.388	2.133
41	M40	60	3.11	1.20	52.6	52.0	0.995	0.972	0.321	2.133
42	M41	50	2.06	1.06	56.9	57.1	1.320	1.329	0.484	1.870
43	M41	50	2.57	1.13	53.0	53.5	1.127	1.149	0.389	1.870
44	M41	60	3.15	1.22	52.7	53.1	0.998	1.014	0.318	1.870
45	M42	50	2.06	1.08	57.5	57.4	1.351	1.347	0.486	1.792
46	M42	50	2.53	1.16	54.2	54.0	1.185	1.176	0.396	1.792
47	M42	60	3.11	1.24	53.4	53.5	1.026	1.033	0.321	1.792

Menu