Visualizing "logarithmus naturalis"

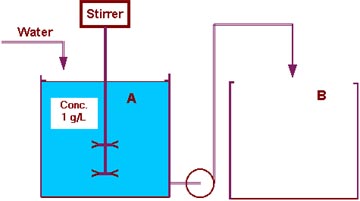
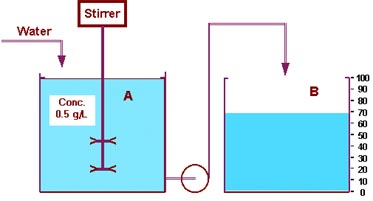
If one is interested in a special dilution factor, such as 2 or 5 or 10, rather than in factors like 2.72 (e1) or 7.39 (e2), a search for the right exponent of the base  e will help. The exponent will no longer be an integer but will become a fraction. The result of a search for the right exponent of the base e is called "logarithmus naturalis" (ln). The attribute "naturalis" shows its connection with natural processes. In a visualized form the logarithmus naturalis of the dilution factor corresponds to the amount of water in the overflow vessel(s), expressed in terms of vessel units. This is demonstrated for a dilution factor of 2.00 in the following figures:

step-size	steps realized	Formula	Dilution factor
1/100	100 %	(1 + 1/100)100	2.70
1/100	80 %	(1 + 1/100)80	2.22
1/100	70 %	(1 + 1/100)70	2.01
1/100	69 %	(1 + 1/100)69	1.99
1/1000	69.3 %	(1 + 1/1000)693	2.00
Instead of an iterative search with percentage of filling use   logarithmus naturalis  for n (up to infinite) steps:
step-size	steps realized	Formula	Dilution factor
1/n	n	(1 + 1/n)n	e
1/n	n * ln 2	(1 + 1/n)n * ln 2	2.00
1/n	n * ln 5	(1 + 1/n)n * ln 5	5.00
1/n	n * ln 10	(1 + 1/n)n * ln 10	10.0

A more common formula for a calculation of a dilution factor of 2.00 is (1 + ln2/n)n. This formula simply uses smaller steps instead of fewer steps. It is easier to convert the folmulas mathematically instead of using a new page with graphic explanation: The fraction in the formula (1 + 1/n)n*ln2 can be multiplied by ln2 to an intermediate form (1 + ln2/n*ln2)n*ln2. Now  n*ln2  is replaced by n again.