Introduction of time

To simplify the question, time was eliminated from the "nut to crack" and the overflow was collected in an equal-sized vessel. In practice a dilution rate (D) and a dilution time (t) are used. D is defined as flow rate (L/h), divided by volume (L), but vessels/h will serve here in the same way. A dilution rate of  D = 1   together with a dilution time  t = 1 h will give the same result as a filling of an equal-sized vessel:

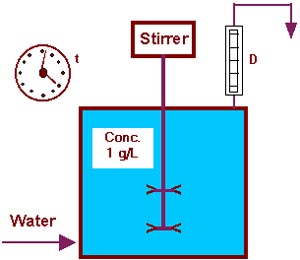
The usual formula for the "nut to crack" reads as follows:   c = c0 * e-Dt  = 1 * e- (1 * 1)  = 0.368. The same result will be reached with a dilution rate of D = 2 vessels/h together with a dilution time t = 0.5 h: c = 1 * e- (2 * 0.5)  = 0.368. Now it is possible to calculate  c,  D  or  t  for any other combination: e.g.  c0 = 40 g/L,  D = 3  and  t = 1.5 h: c = c0 * e-Dt  = 40 * e-(3 * 1.5)  = 0.444 g/L. e.g.  c = 20 g/L,  c0 = 40 g/L,  D = 3   20 = 40 / e3 * t   t = ln2 / 3   t = 0,231 h